Book Review: What Makes Us Smart, by Samuel Gershman

What makes us smart can occasionally make us dumb. But we’re still pretty smart.

I. Inside You Are Two Biases

In his book What Makes Us Smart, Gershman uses a Bayesian¹ framework to sketch a uniquely textured view of cognition, a perspective which sees many “mistakes” in reasoning as perhaps inherent to general intelligences such as ours. These mistakes may not even be mistakes, Gershman argues. Instead, we could consider them the drawbacks of important biases that, while acting as effective guides in the long run, may lead us astray in contrived circumstances (like those set up by logicians and experimenters).

There’s two kinds of these biases: approximation and inductive. But they aren’t biases in the word's pejorative sense; they simply define hard limits of cognition. Approximation biases are probably the more intuitive: when faced with constraints in time, energy, or information, it’s often necessary to arrive at an approximate instead of exact understanding.

Take language, for instance. Gershman describes ambiguity as a trade-off between the informativeness of language and the effort required to understand it. Maximally informative languages like the artificial language Loglan, designed to be as straightforward and unambiguous as possible, complicate the simplest thoughts with overwhelming specificity. As a vivid example, the author cites a Lobjan meeting (Loglan’s successor language) where attendees were served hamburgers—translated “zalvi ke nakni bakni rectu”—which literally means “ground type of male cow meat”. How exhausting! Avoiding ambiguity doesn’t mean we approach total clarity after all. We care about efficient communication, and part of efficiency is keeping things simple. How easy it is to parse language matters.²

Inductive biases, on the other hand, are a result of there being numerous valid ways to make sense of the same data. The problem is echoed by the character Philo from Hume’s Dialogues Concerning Natural Religion:

“...after he opens his eyes, and contemplates the world as it really is, it would be impossible for him at first to assign the cause of any one event, much less of the whole of things, or of the universe. He might set his fancy a rambling; and she might bring him an infinite variety of reports and representations. These would all be possible; but being all equally possible, he would never of himself give a satisfactory account for his preferring one of them to the rest.”

Because it’s possible to generate so many hypotheses that fit the same observation, it’s useful to constrain our hypotheses before making judgments about what we observe. Inductive biases, therefore, limit our “fancy” from getting carried away by the sheer “variety of reports and representations” we might get lost in. If we didn’t have such biases, the space of interpretations for a given set of data is too large to have working explanations ready for use, critically, in guiding action.

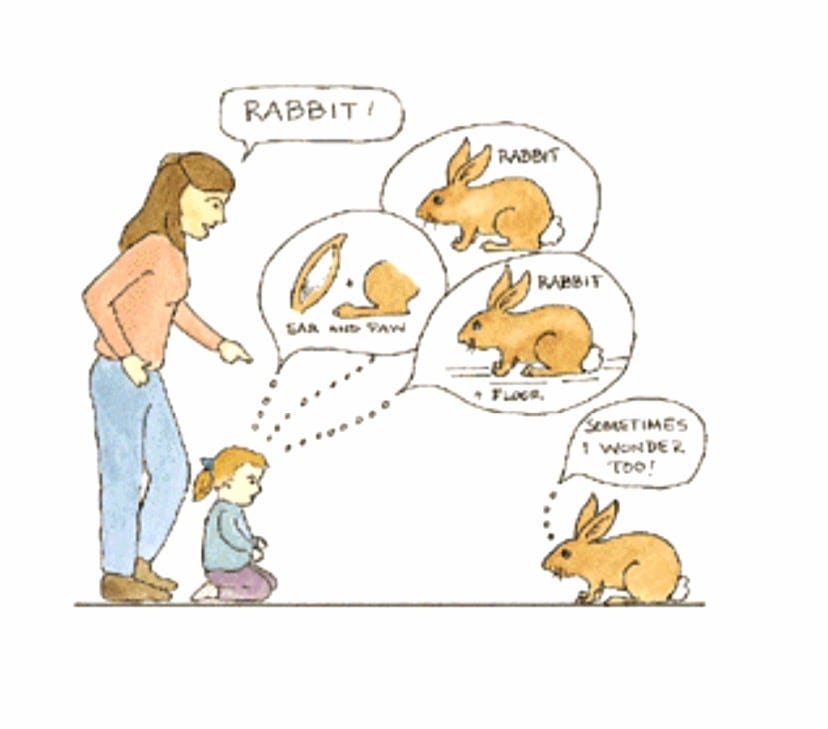
The oft-cited solutions to the gavagai problem are classic illustrations of inductive biases at work in cognition. These are shape and whole-object biases, which structure our perception in early development and help form the basis for learning language. When some perceptual stimulus (i.e. a rabbit) is paired with the spoken word “gavagai”, it’s not, in principle, an easy task to figure out which exact feature of the stimulus the word “gavagai” refers to. Could it be the rabbit’s leg, its ears?

But children don’t confusedly cycle through the options; they realize that “gavagai” likely refers to the whole animal (whole object bias) and that this object name applies to other newly seen, yet similarly-shaped objects (shape bias). Bayes joins this conversation in the context of hierarchical Bayesian learning, in which certain priors act on other priors to constrain the distribution of sensory input a person receives over their lifetime. Shape and whole object biases, as they lie deep in cognition, act on and shape more particular, task-driven priors. In other words, these specific biases help us learn to learn.

II. “How to Never Be Wrong”

Following the examples above, this book can be seen as a tireless taxonomy of Bayesian framings of familiar and unfamiliar biases. If this sounds up your alley, you’ll likely relish the detail, as I did. But because my space here is limited, and I can’t discuss everything, I’ll spend the rest of this review discussing a fascinating chapter on inductive biases, entitled “How to Never Be Wrong”. In it, Gershman raises philosophical difficulties on the progress of science, and provides an interesting Bayesian framework to address these difficulties, a framework that attributes some underlying plausibility to disparate notions like “true selves”, stereotypes, extinction learning, conspiracy theories, and religious belief (not all of which I’ll discuss here).

Our discussion begins in the heavens. Uranus, discovered in 1781, was known to behave rather oddly, frequently deviating from the cosmic course predicted by the then-dominant Newtonian theory of gravity. Two scientists, Le Verrier and Adams, separately showed that these deviations might be caused by some not-yet observed planet whose gravitational influence tugged Uranus from its predicted path. Telescopic observation eventually proved them correct, and they rescued Newton’s theory from an early 19th century disconfirmation, while discovering a new planet in the process: Neptune.

What these two scientists did is what’s known in the science business as an ad-hoc auxiliary hypothesis. When you have a robust central hypothesis like Newton’s theory, any evidence which seems to cast a negative light on it is preferentially explained in terms of lesser auxiliary hypotheses, like those used to construct measurement devices (i.e. theories of optics for making telescopes). Or, one could go even further and posit some unobservable entity to bring the negative evidence to rest, and say there are variables not yet accounted for, posing tentative ad-hoc explanations to save appearances.

Although this strategy worked with Neptune, it didn’t serve Le Verrier so well when he tried to apply it to the unexplained wobble of the planet Mercury around its axis of rotation (otherwise known as its precession). Gershman relays that Le Verrier proposed a hypothetical planet called Vulcan to explain this peculiarity of Mercury, and some astronomers, perhaps inspired by Le Verrier’s previous success, even claimed that they’d seen this planet in their telescopes. But as we know today, Le Verrier’s effort was doomed. There is no planet Vulcan (except for the one that lives in every Trekkie’s heart). The problem of Mercury’s precession was solved eventually, but the solution required more theoretical umph than ad-hoc auxiliary hypotheses could offer—astronomers had to wait for the more drastic revision to Newtonian physics provided by Einstein’s general relativity.

So clearly, there are limits to how helpful ad-hoc auxiliary hypotheses can be. Which leads us to ask, our questions anticipated by Gershman: how should we assign credit or blame to central and auxiliary hypotheses? It can be argued that if ad-hoc auxiliary hypotheses are “allowed” for making theories, our theories can always dodge disconfirmation. If we can use auxiliary hypotheses to brush aside data which darken our central hypotheses, we may never make real scientific progress, progress based on finding deep faults within old frameworks.

But auxiliary hypotheses are nonetheless intuitive and often useful: it seems rational, as Bayesians, to have our theories consist of deep prior belief in our central hypotheses, while having an inductive bias towards proposing auxiliary hypotheses that explain anomalies with high probability. That is, when faced with data we can’t immediately throw out, we tend to accommodate them into our theories using side-explanations, despite how cumbersome our theories may become. And although this sort of intuitive theorizing can be effective, it’s also prone to some ridiculousness, which we’ll see later.

To get to the bottom of this, let’s try to examine hypotheses in isolation, momentarily leaving aside their position in the center or periphery of our theories. We quickly bump into what’s called holism in philosophy of science. This is the idea that there may be no such thing as a hypothesis in isolation. Holism about scientific testing is often called the Quine-Duhem thesis, elegantly described by Peter Godfrey-Smith as the following (from his wonderful book Theory and Reality):

“The idea is that in order to test one claim, you need to make assumptions about many other things. Often these will be assumptions about measuring instruments, the circumstances of observation, the reliability of records and of other observers, and so on. So whenever you think of yourself as testing a single idea, what you are really testing is a long, complicated conjunction of statements; it is the whole conjunction that gives you a definite prediction. If a test has an unexpected result, then something in that conjunction is false, but the failure of the test itself does not tell you where the error is.”

When “the failure of the test itself does not tell you where the error is”, we say that the gathered evidence underdetermines any conclusions we can draw. This might seem an insurmountable obstacle for science. Knowing how experimental data influences specific hypotheses is of paramount importance for the scientist, not to mention for people in their day-to-day. But we might be able to look to probability theory for a solution.

The Bayesian answer to underdetermination involves, instead of treating hypotheses as only either central or auxiliary, dealing with them in a “graded manner”, each hypothesis—every link in Godfrey-Smith’s “complicated conjunction of statements”—taking credit in proportion to how much of the data it’s “responsible” for. Since more central hypotheses take responsibility for more evidence, they tend to be epistemically dug in, and are harder to dislodge than relatively more auxiliary hypotheses. (Equations for this are provided for probability-enjoyers, but for simplicity’s sake, I won’t include them here.)

This picture of belief-updating (as a more down-to-earth form of scientific theorizing) has a flowy relationship between so-called central and auxiliary hypotheses. To start with, we have to consider the prior probabilities of both types of hypotheses, since this value determines how respectively entrenched either type of hypothesis is. The higher the prior probability of the central hypothesis relative to an auxiliary hypothesis, the safer the central hypothesis is, and the blame cast by negative evidence can be shifted to auxiliary parts of the theory. Likewise, if the auxiliary hypothesis has higher prior probability than the central hypothesis, the central hypothesis will have to take the brunt of the disconfirmatory evidence, perhaps leading to cracks that future disconfirmatory evidence widens. So for the Bayesian, the terms “central” and “auxiliary” are a little misleading; the prior probabilities of different parts of a theory are more useful, which we can imagine as a shifting contour map of values assigned to different regions of our theories.

Hold on, you might say—high prior-probability beliefs are more immune to disconfirmation? This seems to justify a form of motivated reasoning, in which we argue for things because we want them to be true, just because we already know them to be true. But that’s not what the Bayesian view argues. Some resistance to disconfirmation is pretty rational, and in line with Bayesian principles. It’s an advantage of such belief-updating principles that they confer stability to our theories, while allowing them to remain receptive to new and persuasive evidence.

One case in which our theories might be overly stable is the popular notion of two layers to personality—our “superficial” and our “true” selves. It seems a widely held view that people, deep down, are good. This is borne out by evidence which suggests that people tend to believe positive personality traits are more “essential to the true self than negative undesirable traits”³, and that people sense they understand someone more deeply the more positive information they are given about them.⁴

So when we witness a person whose true self we believe to be good engage in bad behavior, we tend not to update our belief about their inner goodness. Bad behavior is generally seen as superficial; the strong prior belief that people are deep-down good tends to be relatively immune from disconfirmation. The Bayesian framework would suggest that we discount bad behavior by viewing it as a lapse in judgement caused by situational factors in that person’s life. It hasn’t been worked out experimentally whether people think this way yet, but it’s a nice prediction.

Conspiracy theories are also a case in which a Bayesian touch proves handy, but in a different sense than true selves. Conspiracy theories seem like a morass of auxiliary hypotheses. It’s worth quoting Gershman more extensively here:

“Conspiracy theories are interesting from the perspective of auxiliary hypotheses because they often require a spiraling proliferation of auxiliaries to stay afloat [emphasis mine]. Each tenuous hypothesis needs an additional tenuous hypothesis to lend it plausibility, which in turn needs more tenuous hypotheses, until the theory embraces an enormous explanatory scope. For example, people who believe the Holocaust was a hoax need to explain why the population of European Jews declined by 6 million during World War II; if they claim that the Jews migrated to Israel and other countries, then they need to explain the discrepancy with immigration statistics, and if they claim these statistics were false, then they need to explain why they were falsified, and so on.”

As Gershman points out, the conspiracy theorist often relies on an increasingly complicated set of auxiliary hypotheses to fit data that can be explained far more simply. And using the concepts we’ve built upon so far, the need to accompany every minute detail with a sui generis explanation seems to result from too-relaxed auxiliary hypotheses, resulting in extravagant theories which overfit the data.

Although Gershman presents religious belief in a separate section than conspiracies, citing the greater numbers of people who share those beliefs, it’s hard not to notice the similarities. The same way conspiracy theorists often dismiss credible claims by undermining measurement devices (i.e. media polling), religious creationists may insist on the inadequacy of carbon dating to accurately estimate the age of fossils. But let’s give religious believers more credit. As Bayesians, we’re here to salvage some reasonableness from superficially illogical expressions of human cognition. Could believers in some way be justified in their belief on probabilistic grounds?

One historic argument against religious belief was put forward by Hume, an argument based on the unlikelihood of miracles, anomalous events often taken as evidence for the existence of God. Hume argues that since there will always be far more evidence against miracles than support them, given the wealth of data for the natural laws miracles are supposed to break, unless we’re totally convinced by witnesses testifying to those miracles, we should withhold belief. He goes on to reject the reports of the often uneducated people these tales of miracles tend to arise from. But it may not be as simple as Hume thought.

Gershman points out that the way we take in evidence about miracles matters, that our perception about the impact of the evidence is colored by the deep priors we hold about how the world works. As a religious believer with a higher prior on the existence of God than the existence of natural laws, it will seem reasonable to dismiss evidence for evolution on the basis of one’s conviction that animals created in one form persisted in that shape until the current day. The difficulty in reaching such a person with good empirical evidence (as someone with priors that diverge from creationism) is apparent. However, if the discussion so far has any merit, the Bayesian framework may open up an avenue for persuasion.

If we want to influence the shifting map of priors that make up a person’s world-model, the way to go about it seems to first identify and deal with the outside belt of auxiliary hypotheses before going for the central hypotheses, which people by nature are far more invested in protecting. By prying away auxiliary hypotheses one by one, we may manage to expose the central hypothesis at the core of their worldview. This obviously requires a lot of time and effort, and often isn’t achievable in the course of a short debate or discussion. Effective persuasion requires an abundance of patience, along with caution not to touch the live-wire that is most people’s deeply held beliefs. And if we ever find ourselves losing patience in the midst of this work, it’s good to remember that people do, in fact, change their minds.

III. Closing

To do justice to his claims, it’s worth closing with the author’s caveats. One is that there are other frameworks besides Bayes’ that explain belief-updating quite well. Gershman also addresses worries (which certainly cropped up in my own mind) of whether a Bayesian model of cognition really describes what goes on in the human brain. Furthermore, the falsifiability of Bayesian models is discussed, a concern arising from their very broad scope. Perhaps Bayesian models, because they can be used to explain so many quirks of cognition, really explain nothing. But Gershman points out that if we’re given (or have experimentally imposed) a prior and likelihood, the model predicts just one posterior, so measuring a posterior different from the one predicted serves to falsify a Bayesian model.

Despite how lofty the goals of this book may have sounded in my review, Gershman’s expressed intent is relatively grounded. There’s a comment he writes in the chapter I present which speaks to the broader aims of the book. His goal is to

“…show that evidence for robustness to disconfirmation does not by itself indicate irrationality; it is possible to conceive of a perfectly rational agent who exhibits such behavior……The point here is not to establish whether people carry out exact Bayesian inference (they almost surely do not) but rather show they are not completely arbitrary.”

And according to this outline of his general aim, I think he’s certainly achieved his goal, or come very close to it.

The simple beauty of this book is that it shows that many cognitive strategies have certain built-in tradeoffs that, despite looking out for them, stay resistant to correction because they tend to be good-enough policies in the long run. Rational thinking (exemplified by Bayes’ rule) doesn’t mean correct thinking so much as reasonable thinking, which while often wrong, is still an optimal means of working through inevitable constraints to find truths about the world. And it may be that as we instill the flexibility of our cognitive performance into machines, AI could make, almost by necessity, the sort of systematic mistakes we do.

This book also reminded me why I fell in love with cognitive science to begin with, that it wasn’t so much for improving how I think as for uncovering general mechanisms of thought. Even if we don’t accept the view that Bayesian models tell us what goes on in our own brains, nonetheless—what light streams through the window Gershman opens! More people should read this book for a thorough look at how much power computational methods offer to explain mind and behavior. I’ll definitely be returning to it in the future.

1. You may have heard the expression, famously popularized by Sagan, that “extraordinary claims require extraordinary evidence”. This may be regarded as a version of the Bayesian’s mantra, inspired by that simple yet powerful theorem on the updating of prior beliefs upon their encounter with evidence; this interaction between priors and data generates what are called posterior beliefs.

To restate the “Sagan standard” in Bayesian terms — the larger the difference from some prior to a posterior, the more compelling the evidence must be.

2. Gershman goes on to explain this efficiency trade off in information-theoretic terms, as the balance between compressibility (shorter description length means low effort parsing) and expressiveness (how many different ideas can be given utterance). Both speakers and listeners want to expend the least effort while apprehending as wide a range of meanings as possible. But if something is overly compressed, too many meanings may map onto the same expression. Ambiguity is tolerated in language so long as it’s resolved by context.

3. https://pubmed.ncbi.nlm.nih.gov/15536247/

4. http://existentialpsych.sites.tamu.edu/wp-content/uploads/sites/152/2018/11/1948550617693061.pdf